Isokron kurve

Har du besøkt Vitensenter Nordland? I så fall har du kanskje sett denne gjenstanden. Det er en utstilling som viser en kurve med den egenskapen at uansett hvor du drar en kule på kurven og slipper, så bruker den like lang tid ned til bunnen.

Dersom du drar to kuler til hver sin ende, selv med ulikt utslag, så vil kulene likevel alltid møtes samtidig på midten. Kurven kalles en isokron kurve, fra de greske ordene isos - lik- og kronos - tid. Et passende navn, altså.

Jeg vet ikke hvorfor, men det var denne utstillingen som fenget meg mest ved første gangs besøk på Vitensenteret. På kvelden fikk jeg ikke sove, og jeg ble liggende å gruble. Kunne jeg klare å utlede formler?

Problemet lå og kvernet i hjernebarken et par dager før jeg fikk et eureka-øyeblikk. Gjennombruddet kom da jeg innså at under ideelle forhold, der man ser bort fra luftmotstand, friksjon og rotasjonsenergi til kulen, så vil kulen bare oscillere frem og tilbake til lik høyde der man slapp den, og uansett hvor man slipper den så vil den bruke like lang tid per oscillasjon.

Fra fysikken har vi et annet system som har den samme egenskapen, og det kalles en harmonisk oscillator. Systemet er et yndet studieobjekt i fysikken, eller når man lærer om differensialligninger i matematikken.

En harmonisk oscillator er beskrevet av en differensialligning på formen

$$\ddot{s} + \omega^2 s = 0$$

der $s$ er utlaget fra en likevektsposisjon og $\omega$ er vinkelfrekvensen, som for øvrig har følgende relasjon til svingeperioden $T$

$$\omega = \frac{2\pi}{T}$$

De to prikkene over s indikerer at man deriverer to ganger med hensyn på tid.

En masse festet til en elastisk fjær er et typisk eksempel på en harmonisk oscillator.

Utledning

Vi tar utgangspunkt i ligningen til en harmonisk oscillator $\ddot{s}+\omega^2 = 0$ og Newtons andre lov,
$F = ma$. Siden $s$ er en posisjon, og den andre tidsderiverte av posisjon er aksellerasjon, så har vi at $a = \ddot{s}$.

Vi setter dette inn i Newtons andre lov og får

$$F = ma = m \ddot{s} = -m\omega^2 s$$

Den eneste kraften som påvirker systemet er gravitasjonen.

$$F_g = -mg \sin \theta$$

der $g$ er den gravitasjonelle aksellerasjonen og $\theta$ er vinkelen mellom x-aksen og tangentlinjen til kurven på posisjon $s$. Når $\theta$ er 0 er tangentlinjen horisontal, noe som betyr at vi er helt i bunnen av kurven. Når $\theta$ er $\pm \frac{\pi}{2}$ er tangentlinjen vertikal, og vi er da øverst i kurven på henholdsvis høyre og venstre side.

Utrykket har et minustegn for å indikere at kraften virker i negativ y-retning.

Ved å sette $F = F_g$ så kan vi utlede at

$$s = \frac{g}{\omega^2} \sin \theta.$$

Denne ligningen sier bare noe om hvor langt fra bunnen langs kurven vi er, der negativ verdi betyr at vi er på venstre side av kurven. Avstanden fra bunnen og til høyre topp blir da $\frac{g}{\omega^2}$ når man måler langs kurven, og lengden på hele kurven blir dermed to ganger dette, $\frac{2g}{\omega^2}$.

Vi må jobbe litt mer for å finne formler for å tegne kurven i et xy-koordinatsystem.

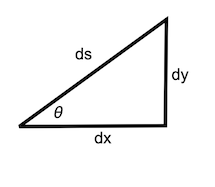
Dersom vi ser på et infinitisimalt linjesegment av kurven, dvs. zoomer inn på et lite område av kurven til linjesegmentet $ds$ er tilnærmet en rett linje, så kan vi finne relasjoner mellom linjesegmentet, vinkelen $\theta$ og to infinitisimale lengder $dx$ og $dy$ i henholdvis x- og y-retning. Se illustrasjonen over.

Det er en rettvinklet trekant, og vi får følgende to ligninger,

$ds = \frac{dx}{\cos \theta}$ og $ds = \frac{dy}{\sin \theta}$

Vi har fra før utledet at $s = \frac{g}{\omega^2} \sin \theta$, og deriverer vi dette med hensyn på $\theta$ så finner vi et utrykk for $ds$,

$$ds = \frac{g}{\omega^2} \cos \theta d \theta.$$

Vi erstatter dette utrykket for $ds$ inn i de to ligningene med $dx$ og $dy$ og får

$$dx = \frac{g}{\omega^2} \cos^2 \theta d \theta$$

og

$$dy = \frac{g}{\omega^2} \sin \theta \cos \theta d \theta = \frac{g}{2 \omega^2} \sin 2\theta d \theta$$

Ved å integrere $dx$ og $dy$ med hensyn på $d \theta$ så får vi endelig to formler vi kan bruke for å tegne kurven, parametrisert ved vinkelen $\theta$,

$$x = \frac{g}{4 \omega^2}(2 \theta + \sin 2 \theta) + C_x$$

$$y = -\frac{g}{4 \omega^2} \cos 2 \theta + C_y$$

Graf av resultatet

Vi definerer en funksjon i Mathematica kalt isochrone og plotter den med funksjonen ParametricPlot. For enkelhets skyld setter vi den gravitasjonelle aksellerasjonen og vinkelfrekvensen til 1.

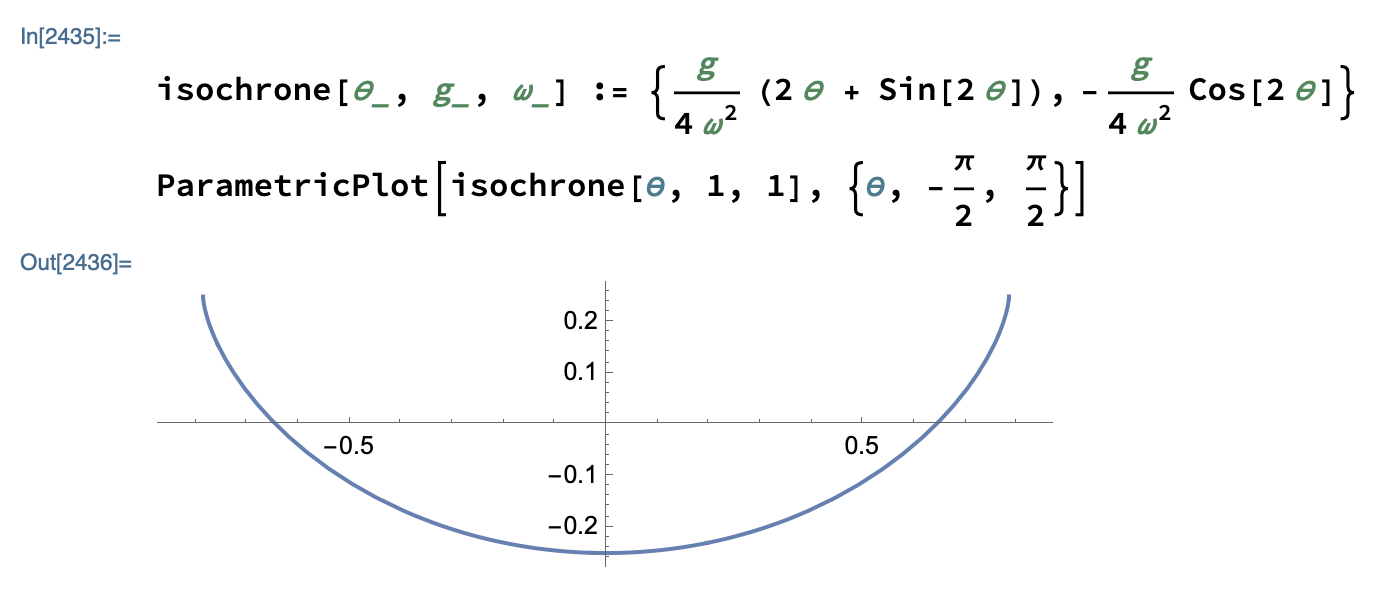
Kurven ser ut til å stemme godt overens med bildet fra Vitensenteret.

Vi utledet også en formel for lengden på kurven, $\frac{2g}{\omega^2}$. For $g$ og $\omega$ lik 1 skal det gi lengde 2. I Mathematica kan vi bruke funksjonen ArcLength for å finne lengden på en kurve. Svaret blir 2, så det støtter oppunder at formlene er riktige.

En isokron kurve er en sykloide

Fra starten av ante det meg at kurven var en sykloide. En sykloide er en kurve som dannes ved at man følger et punkt på en sirkel i det sirkelen ruller i konstant fart uten å gli på underlaget. Jeg har laget en animasjon i Mathematica som illustrerer hvordan det ser ut.

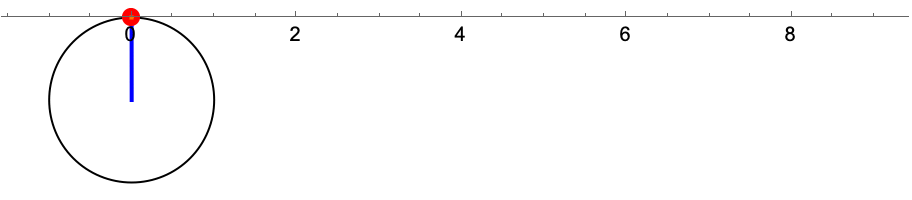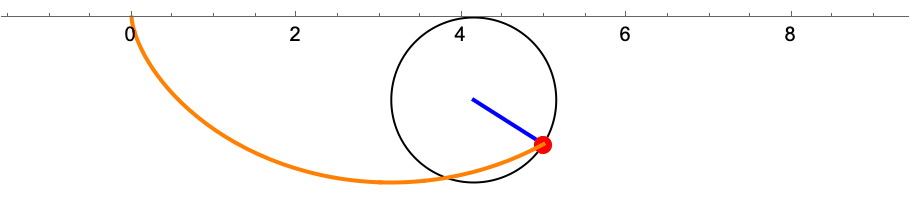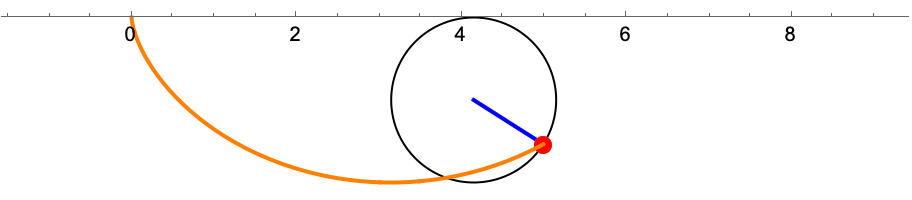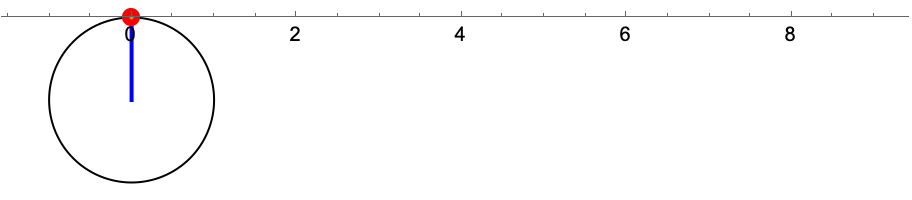
En sykloide der sirkelen ruller på undersiden av aksen har følgende parametrisering

$$x = R(\phi - \sin \phi)$$

$$y = -R(1 - \cos \phi)$$

Ved direkte sammenligning av formlene for en sykloide med formlene vi utledet for en isokron kurve, så kan vi se at en isokron kurve er en sykloide som er generert av en sirkel med radius

$$R = \frac{g}{4 \omega^2}$$

Tiden det tar for en kule å rulle ned til midten

Ut i fra forrige formel kan vi regne ut perioden som kulen vil oscillere med som en funksjon av den gravitasjonelle aksellerasjonen $g$ og radiusen $R$ til sirkelen.

Ved å sette inn $\omega = \frac{2 \pi}{T}$ kan vi løse for tiden det tar for ballen å rulle frem og tilbake til den når utgangspunktet.

$$T = 4 \pi \sqrt{\frac{R}{g}}$$

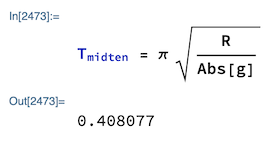
Tiden det tar for en kule å rulle ned til midten når man slipper kulen fra et hvilket som helst sted på kurven vil da være en fjerdedel av dette,

$$T_{midten} = \frac{T}{4} = \pi \sqrt{\frac{R}{g}}$$

Neste gang jeg dro til Vitensenteret gjorde jeg en kjapp måling av avstanden mellom de øverste punktene på kurven. Det tilsvarer avstanden som en genererende sirkel ville ha rullet for ett omløp, altså omkretsen til sirkelen.

Jeg målte 104 centimeter mellom punktene. Sannsynligvis ikke en veldig nøyaktig måling, men det lar oss estimere radiusen til den genererende sirkelen

Vi vet også den gravitasjonelle aksellerasjonen

Og med disse to verdiene kan vi regne ut tiden det tar for en kule å rulle ned til midten

Vi må huske på at dette kun er en teoretisk og ideell modell. I virkeligheten vil det ta noe lenger tid på grunn av friksjon og luftmotstand, og fordi noe energi går til rotasjonsenergi i kulen.

Det kunne likevel ha vært en interessant øvelse å gjøre tidsmålinger for å se hvor godt teori samsvarer med praksis.

Farten til kulen når den kommer ned til midten

Vi vet fra fysikken at når et objekt faller ned i et gravitasjonelt potensial så vil potensiell energi veksles til kinetisk energi. Formlene for potensiell- og kinetisk energi er

$$E_p = mgh$$

$$E_k = \frac{1}{2} mv^2$$

Dersom vi setter disse lik hverandre så kan vi finne en formel for fart som funksjon av høyden vi slipper kulen fra, målt fra bunnen av kurven

$$v = \sqrt{2gh}$$

Høyden vet vi at på det høyeste punktet er lik diameteren til den genererende sirkelen, så den teoretiske farten kulen vil ha når den når bunnen av kurven er

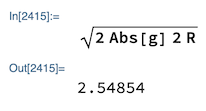
En modell for utstillingen på vitensenteret

Ved å skrive om formelen $R = \frac{g}{4 \omega^2}$ så kan vi finne et utrykk for vinkelfrekvensen til systemet på vitensenteret

$$\omega = \sqrt{\frac{g}{4 R}}$$

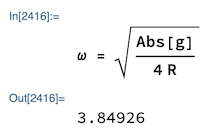
Vi kan nå definere en funksjon i Mathematica for vinkelen til systemet som funksjon av tiden, samt posisjon som funksjon av tiden. Vi plasserer origo for koordinatsystemet i bunnen på kurven.

Vi har altså laget oss en modell for systemet på Vitensenteret. La oss gjøre et par kontrollberegninger for å sjekke om resultatene er plausible

Her kan vi se at posisjonene ved tidene $t = 0$ og $t = 2 T_{midten}$ er $\{ -0.52, 0.331042 \}$ og $\{ 0.52, 0.331042 \}$. Det samsvarer godt i og med at bredden til kurven er 1.04 meter og høyden er to ganger radius.

Ved $t = T_{midten}$ er posisjonen veldig nær $\{0, 0\}$. At den ikke er helt nøyaktig er på grunn av avrundingsfeil i datamaskinen. Også dette resultatet samsvarer godt.

Til sist tar vi en kontroll på fart. Fart er den deriverte av posisjon, så vi lar Mathematica finne den deriverte av posisjonsfunksjonen.

Tatt i betraktning avrundingsfeil så finner vi at farten er 0 ved $t = 0$ og $t = 2 T_{midten}$, og i bunnen er farten 2.54854 meter per sekund, akkurat som forventet fra tidligere beregninger.

Jeg tror vi kan si oss sånn høvelig fornøyd med modellen 👍

Det isokrone problem

Vi har i løpet av dette blogginnlegget løst det som er kalt “det isokrone problem”. Historisk var det Christiaan Huygens som først skal ha løst det, i 1659, i sin jakt på en bedre pendel-klokke.

Harmoniske oscillatorer har en fast periode som egner seg godt til tidtaking. Som dere kanskje vet så er en pendel-klokke som følger en sirkulær kurve kun tilnærmet en harmonisk oscillator for små vinkelutslag. Hvis man drar pendelen for langt ut til siden så vil den ikke ha en harmonisk bevegelse og er dermed ikke egnet som klokke. Perioden til en slik pendel-klokke vil heller ikke være konstant etter som den mister energi til friksjon og luftmotstand.

Dersom man får bygget en pendel-klokke som på ett eller annet vis følger en sykloidisk kurve, så vil den være en harmonisk oscillator selv for større utslag og selv om pendelen gradvis mister energi. På alle måter en bedre klokke.

Dessverre så viste det seg at det i praksis var vanskelig å konstruere en slik pendel-klokke.